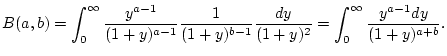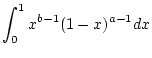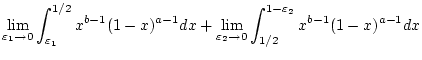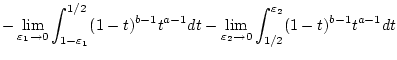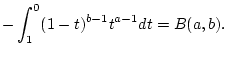Aufgabe 2.12.2.1
Wir haben in diesem Punkt für gegebenenfalls uneigentliche Integrale
bei der Substitution von Variablen und beim partiellen Integrieren
formal genauso gerechnet wie mit eigentlichen Riemann-Integralen.
Die Korrektheit dieses Vorgehens muß im einzelnen nachgeprüft werden.
So muß z.B. die Rechnung für (
2.12.2.1) im Fall
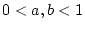
detailiert wiefolgt aussehen
Verifizieren Sie auf gleichem Wege alle Rechnungen dieses und der
folgenden Abschnitte, insbesondere die partiellen Integrationen, detailiert
auf Korrektheit unter Berücksichtung der uneigentlichen Integrale!
![]()
![]() . Dann gilt
. Dann gilt
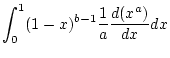
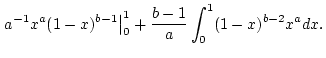
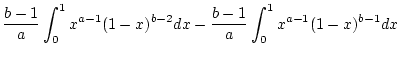
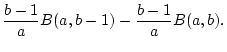
![]() in (2.12.1.1),
so erhält man
in (2.12.1.1),
so erhält man