Für absolut konvergente Reihen gilt der Umordnungssatz: Konvergenz und Wert der Reihe sind unabhängig von der Ordnung der Summanden.
Wir betrachten zunächst den Fall
![]() . Angenommen,
die Reihe
. Angenommen,
die Reihe
![]() konvergiert absolut. Nach
Satz 1.6.3.6 konvergieren damit auch
konvergiert absolut. Nach
Satz 1.6.3.6 konvergieren damit auch
![]() und
und
![]() . Auf diese Reihen ist Satz
1.3.2.1 anwendbar und es gilt
. Auf diese Reihen ist Satz
1.3.2.1 anwendbar und es gilt
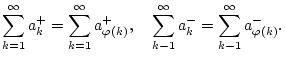
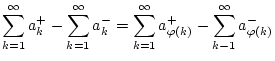 |
|||
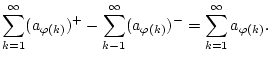 |
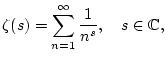
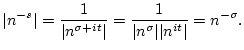
Die Riemannschen Zetafunktion ![]() spielt in den verschiedensten
mathematischen Teilgebieten eine zentrale Rolle. Mit ihr ist auch
das wohl gegenwärtig berühmteste offene mathematische Problem verbunden,
nachdem alle Nullstellen dieser Funktion auf der Gerade
spielt in den verschiedensten
mathematischen Teilgebieten eine zentrale Rolle. Mit ihr ist auch
das wohl gegenwärtig berühmteste offene mathematische Problem verbunden,
nachdem alle Nullstellen dieser Funktion auf der Gerade
![]() liegen. Dies ist eines der sieben sogenannten Millenium-Probleme,
für deren Lösung das Clay Mathematics Institute einen Preis von jeweils
1.000.000 US$ ausgeschrieben hat.
liegen. Dies ist eines der sieben sogenannten Millenium-Probleme,
für deren Lösung das Clay Mathematics Institute einen Preis von jeweils
1.000.000 US$ ausgeschrieben hat.