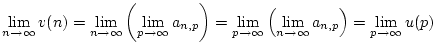Next: Der Satz über das
Up: Das Vertauschen von Grenzwerten
Previous: Das Vertauschen von Grenzwerten
Contents
Es sei 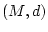 ein metrischer Raum. Wir betrachten (Doppel)folgen
ein metrischer Raum. Wir betrachten (Doppel)folgen
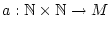 mit den Elementen
mit den Elementen
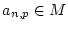 für
für
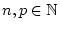 . Angenommen, für jedes
. Angenommen, für jedes
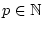 bzw. für jedes
bzw. für jedes
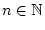 existieren die Grenzwerte
existieren die Grenzwerte
Weiterhin seien die beiden Folgen
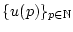 und
und
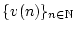 konvergent. Man kann sich dann
die Frage stellen, ob
gilt, d.h. ob man die Ordnung der Grenzwerte
konvergent. Man kann sich dann
die Frage stellen, ob
gilt, d.h. ob man die Ordnung der Grenzwerte
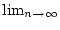 und
und
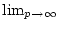 vertauschen kann.
vertauschen kann.
Das folgende Beispiel zeigt, daß diese Frage im Allgemeinen negativ
beantwortet werden muß.
Beispiel 2.2.1.1
Es sei
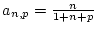
mit
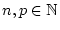
.
Dann gilt offensichtlich
Daraus folgt
2003-09-05
![]() ein metrischer Raum. Wir betrachten (Doppel)folgen
ein metrischer Raum. Wir betrachten (Doppel)folgen
![]() mit den Elementen
mit den Elementen
![]() für
für
![]() . Angenommen, für jedes
. Angenommen, für jedes
![]() bzw. für jedes
bzw. für jedes
![]() existieren die Grenzwerte
existieren die Grenzwerte