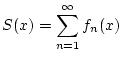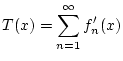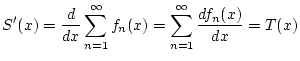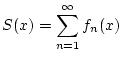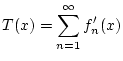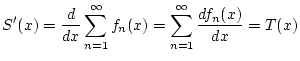Next: Das Vertauschen von Ableitung
Up: Zum Vertauschen von Grenzwert
Previous: Die Differentation von Grenzfunktionen
Contents
Satz 2.6.2.1
Wir betrachten eine Folge von Funktionen
![% latex2html id marker 25771
$ f_{n}\in C^{1}([a,b],\mathbb{K}^{d}) $](img1161.png) ,
,
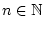 ,
so daß zum einen die Funktionenreihe
existiert und desweiteren die Reihe der Ableitungen
konvergiert. Dann gilt
,
so daß zum einen die Funktionenreihe
existiert und desweiteren die Reihe der Ableitungen
konvergiert. Dann gilt
![% latex2html id marker 25781
$ S\in C^{1}([a,b],\mathbb{K}^{d}) $](img1166.png) und
und
2003-09-05