Drittmittelprojekte

• Principal Investigator: Prof. Dr. Guido Schneider, JProf. Dr. Xian Liao (KIT)
• Funding Period: August 2023 to June 2027
• Summary: Ein Ziel ist es, die Gültigkeit des Whitham-Approximationsergebnisses für allgemeine wellenartige Gleichungen zu zeigen und die Ergebnisse von Gevrey-Räumen auf Sobolev-Räume zu übertragen. Wir planen, die Länge der möglichen Approximationszeiten von Amplitudengleichungen für eine Reihe von integrierbaren Systemen über die natürlichen Zeitskalen hinaus zu verbessern.

• Principal Investigator: Prof. Wolf-Patrick Düll
• Funding Period: November 2022 to Oktober 2025
• Summary: The goal of the project is the justification of NLS approximations for the three-dimensional
  water wave problem with surface tension by proving estimates of the error between exact
  solutions to the water wave problem and their formal approximations obtained via NLS
  equations in the physical relevant scales.

• Principal Investigator: Prof. Dr. Guido Schneider
• Collaborators: Jun.-Prof. Dr. Marco Oesting
• Funding Period: September 2022 to December 2025
• Summary: We consider multiple scaling problems for which effective asymptotic models do exist. These regular limit systems very often can be obtained via singular perturbation techniques. These approaches allow for an effective numerical simulation and are less expensive than direct simulations of the original sys- tems. These tools have been applied successfully to various deterministic and stochastic multi-physics problems.
  There are three goals of this project.
  
  1. We would like to use the regular limit systems for an effective simulation of stochastic multiple scaling multi-physics problems. In order to do so the approach for stochastic systems has to be extended from toy problems to real world applications.
  
  2. We would like to use the regular limit systems for an effective uncertainty quantification. Beside the control of noise in pattern forming systems we plan to quantify uncertainty for highly oscillatory systems via averaging or normal form techniques. We would like to extract stable objects such as modulating fronts from an uncertain background.
  
  3. We would like to continue our research about the effective learning of PDE Dynamics through ar- tificial neural networks from deterministic multiple scaling problems to stochastic multiple scaling problems. 

• Principal Investigator: Prof. Dr. Guido Schneider
• Funding Period: July 2019 to June 2024
• Summary: We are studying dispersive systems in periodic media and we are interested in the existence and non-existence of localized structures, such as time-periodic standing pulses or quasiperiodic moving modulating pulses. A prototypical underlying dispersive system is the cubic nonlinear Klein-Gordon equation

  

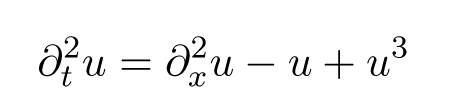
  on a one-dimensional periodic metric graph like, e.g., the periodic necklace graph. Due to their dispersion relation periodic metric graphs are used as models for more complex physical structures such as photonic crystals, nano-tubes or graphene. Even for constant coefficient linear differential equations like the Klein-Gordon equation, periodic metric graphs like the necklace graph may have explicitly computable spectral gaps.
  
  For the construction of
  (i) time-periodic standing pulses
  (ii) time-quasiperiodic moving pulses
  
  we will be using either variational methods or spatial dynamics, invariant manifold theory, and normal form transformations. Despite their fundamental differences, both methods rely on very good control of the Floquet-Bloch spectrum of the underlying linearized differential operator. Whereas the spatial dynamics, invariant manifold and normal form theory typically produces small solutions bifurcating from trivial solutions, the variational tools may lead to large solutions. In addition to one-dimensional periodic graphs we also envisage to study dispersive systems on the real line (e.g., the cubic Klein-Gordon equation) with spatially periodic coefficients.
  
  As a complementary goal we intend to prove also non-existence and non-persistence results for localized structures. This means that we plan to prove dispersive decay estimates for prototypical systems like the nonlinear Schrödinger or nonlinear Klein-Gordon equation on periodic metric graphs. Such decay estimates may lead to global-in-time decay to the zero solution starting from small initial data. Such a result excludes the existence of small bifurcating solutions. It may also be used to show that compactly supported breather solutions do not persist if initial data are perturbed by a small amount of dispersive modes.

• Principal Investigator: Prof. Guido Schneider
• Funding Period: 01.07 2019 - 30.06.2022
• Summary: Wir betrachten musterbildende Systeme mit Erhaltungsgleichungen in unendlich langen zylindrischen Gebieten in der Nähe der ersten Instabilität. Mit Hilfe eines Multiskalenansatzes können Ginzburg- Landau artige Amplitudensysteme hergeleitet werden. Diese sollen verwendet werden, um globale Existenz von Lösungen in der Nähe des instabilen Ursprungs zu zeigen. Anwendungen sind das Marangoni-Problem, der Fluß über eine schiefe Ebene oder das Faraday-Problem. 

• Principal Investigator: Prof. Dr. Guido Schneider
• Collaborators:Prof. Dr.-Ing. Wolfgang Nowak, Dr.-habil. Sergey Oladyshkin, Dr. Björn de Rijk
• Funding Period: July 2019 to June 2022
• Summary: We aim to exploit the learning abilities of ANNs in order to accelerate PDE simulations by using structural knowledge of the underlying PDE. In many time-dependent PDE problems we know for structural reasons (e.g. the presence of symmetries, localizations or oscillations) that the time-consuming part of simulations appears over and over again, but is of very similar nature and is therefore beneficial to learn. Thus, we expect that learning this part of the behavior and replacing it in the simulations by an adaptively used ML ‘black box’ leads to a significant reduction of simulation time.

• Principal Investigator: Apl. Prof. Dr. Wolf-Patrick Düll
  Research Associate: Max Heß M. A.
• Funding Period: 1 April 2017 to 31 March 2020
• Summary:1968 leitete Zakharov die Nichtlineare Schrödinger-Gleichung (NLS-Gleichung) als formale Approximationsgleichung her, um die Evolution der Einhüllenden von oszillierenden wellenpaketartigen Lösungen des Wasserwellenproblems zu beschreiben. Die mathematisch rigorose Rechtfertigung der Gültigkeit dieser Approximation ist seit mehr als vier Jahrzehnten ein offenes Problem. In den letzten Jahren wurde die NLS-Approximation für das Wasserwellenproblem ohne Oberflächenspannung gerechtfertigt. Das Ziel dieses Projektes ist die Rechtfertigung der NLS-Approximation für das Wasserwellenproblem mit Oberflächenspannung durch Beweisen von Abschätzungen des Fehlers zwischen exakten Lösungen des Wasserwellenproblems und deren mittels der NLS-Gleichung erhaltenen formalen Approximationen in den physikalisch relevanten Längen- und Zeitskalen der NLS-Gleichung. Das fundamentale Werkzeug zum Erlangen solcher Abschätzungen soll eine vom Antragsteller vor Kurzem entwickelte Methode sein, die es ermöglicht, die NLS-Approximation nicht nur für semilineare, sondern auch für quasilineare dispersive Systeme zu rechtfertigen.

Das Graduiertenkolleg 1838 ist eine Kooperation der Universitäten Stuttgart und Tübingen. Principal Investigatiors sind Prof. Marcel Griesemer (Sprecher / Stuttgart), Prof. Guido Schneider (Stuttgart), Prof. Timo Weidl (Stuttgart), Prof. Stefan Teufel (Stuttgart), Prof. Chrisitian Hainzl (Stuttgart) und Prof. Christian Lubich (Stuttgart).

Dauer: 10/2013 bis 09/2019

• Principal Investigator: Prof. Dr. Guido SchneiderResearch Associate: Dipl.-Phys. Dipl.-Math. Tobias Haas
• Funding Period: July 2015 to June 2019
• Summary: Approximation by modulation, envelope or amplitude equations plays a fundamental role in the understanding of complex systems. Famous examples are the Korteweg-de Vries (KdV) approximation of the water wave problem, the Ginzburg–Landau approximation for pattern-forming systems, or the nonlinear Schrödinger (NLS) approximation in nonlinear optics. In spite of faster and faster computers they are still the starting point of the analysis of the qualitative behavior of many complex systems. It is widely believed that the formally derived amplitude equations always make correct predictions about the dynamics of the original system. In fact, recent decades have seen proofs of many rigorous approximation results. However, there are many pairs of amplitude equations and classes of original systems for which it has not yet been possible to establish such an approximation result. In this project we would like to concentrate on results that show that in various situations formally derived amplitude equations do NOT make correct predictions about the dynamics of the original system.
  
  A) We plan to establish rigorous estimates showing that the (resonant) four wave interaction system fails to describe the dynamics of the water wave problem with low surface tension. It will be the first rigorous counterexample for an amplitude equation making wrong predictions on the natural time scale of the approximation without imposing spatially periodic boundary conditions on the original system.
  
  B) Similarly, we would like to prove that the NLS equation, the KdV equation, and Whitham's modulational system do not correctly describe wave number modulations of the family of traveling periodic surface water waves in various parameter regimes.
  
  C) By means of numerical experiments we would like to acquire evidence for the failure of a number of amplitude equations outside the analytically established range of validity, i.e., in cooperation with the numerics groups we would like to acquire evidence that the established range of validity is sharp.
  The long-term goal of this project is to establish a catalog of criteria for the failure of amplitude equations in order to prevent the misuse of this reduction method.

• Principal Investigator: Prof. Dr. Guido Schneider, Prof. Dr. Katharina Schratz
• Funding Period: July 2015 to June 2019
• Summary: A summary is available here

• Antragsteller: Prof. Dr. Guido Schneider und PD Dr. Wolf-Patrick Düll
• Projektbearbeiterin: bis 30.11.2014 Dipl.-Math. Alina Hermann
• Förderzeitraum: Dezember 2012 bis November 2015
• Zusammenfassung:  Die langsame zeitliche und räumliche Modulation periodischer Wellenzüge nichtlinearer Wellengleichungen kann formal durch die Whitham-Approximation beschrieben werden. So spielt sie eine wichtige Rolle bei der Beschreibung von sogenannten Monsterwellen. Die Whitham-Approximation kann mittels eines Multiskalenansatzes hergeleitet werden. Bislang ist nur in absoluten Spezialfällen bekannt, dass diese Näherung die Wirklichkeit richtig wieder gibt. Denn durch die formale Herleitung ist keineswegs klar, dass sich das Originalsystem so verhält, wie durch die Näherungsgleichung vorhergesagt. Es existieren zahlreiche Gegenbeispiele, bei denen dies nicht der Fall ist.Die Anzahl der auftretenden generischen universellen Modulationsgleichungen ist stark begrenzt. Im räumlich homogenen Fall sind dies bei Vorliegen von Dissipation die Ginzburg-Landau-Gleichung und bei Energieerhaltung die KdV-Gleichung und die Nichtlineare Schrödinger-Gleichung. Im räumlich periodischen Fall sind dies bei Vorliegen von Dissipation zusätzlich die Phasendiffusion-Gleichung und die Burgers-Gleichung und bei Energieerhaltung eben die Whitham-Gleichungen. Für die aufgeführten Modulationsgleichungen existiert bis auf die Ausnahme der Whitham-Gleichungen eine umfangreiche Theorie, wann diese die Wirklichkeit richtig beschreiben. So ist die Whitham-Approximation die letzte der generischen universellen Multiskalen-Approximationen, für welche bislang keine einigermaßen zufriedenstellende Theorie bezüglich ihrer Gültigkeit existiert. Das Ziel dieses Forschungsprojektes soll es daher sein, diese wichtige Frage zu klären.

• Principal Investigator: Prof. Dr. Guido Schneider
• Research Associate: Dr. Markus Daub
• Funding Period: May 2013 to April 2015
• Summary: It is the goal of this project to analyze and to extend various models used and derived by partners within PN1. Moreover, some cooperations of SimTech 1 will be continued. In particular, we will concentrate on
  the following problems. These are:
  
  A) The analysis and extension of a self-consistent embedded cell model considered by the group of Prof. Schmauder for the computation of stress-strain curves for metal ceramic composites. It is the major
  goal of the First sub-project to prove the convergence of the underlying iterative numerical process and to extend the approach to time-periodic loading.
  
  B) The analysis and extension of dissipative micro-macro models of electro-magneto mechanics considered by the group of Prof. Miehe. The major goal is a mathematical existence theory and the justification of a number of models in dissipative electro-magneto mechanics.
  
  C) An extension of the integration time of the particle model developed for the description of receptor clustering on cell membranes in cooperation with the group of Prof. Wunderlich. A transfer of the approach to problems in PN1 is envisaged.

• Principal Investigator: Prof. Dr. Guido Schneider
• Research Associate: Markus Daub
• Funding Period: May 2008 to April 2013
• Summary:  Apoptosis is one form of programmed cell death in a multicellular organism. It involves a series of biochemical processes, namely so called protease signalling networks. The modeling of such processes is so far mainly done by reaction equations, leading to a low-dimensional system of ODEs, however with a relatively high-dimensional parameter set. For the description of apoptosis the ODE model should be of a bistable form.
  It is the first purpose of this project to extend the used models in various directions, as there are spatially distributed systems, the inclusion of delays into the reaction and uncertainties in the modeling. The analysis and simulation of these extended models is complicated by a number of mathematical problems, as there are singularly perturbed systems and low regular solutions with respect to time and space.
  Since each mathematical model needs to be associated with a purpose of use, the most detailed model is not automatically also the best one. For qualitative predictioness, for example to guarantee the existence of a bistable situation via bifurcation analysis, very often only low preciseness is necessary. In order to optimize the balance between preciseness and computation time we plan to unitize the models in submodels desribing the dynamics in different spatial domains. We expect that the dynamics in the spatial domains is dominated by different effects as transport, diffusion or reaction. In order to do the separation mathematical criteria for the choice of the submodel has to be established. An error-adapted choice of models can considerably reduce the computation time.
  As the purpose of use of the models we will concentrate on bifurcation analysis and long term error estimates which should be of the order of the uncertainties in the modeling. Hence the description of apoptosis is one model where these criteria will be established in order to start with a theory for more general situations.

• Antragsteller: Prof. Dr. Guido Schneider
• Projektbearbeiter:  von Januar 2010 bis Juli 2011 Christopher Chong, von Dezember 2011 bis Dezember 2012 Alina Spitz
• Laufzeit: Januar 2010 bis Dezember 2012
• Zusammenfassung: Die Nichtlineare Schödingergleichung (NLS) beschreibt näherungsweise die Evolution der Einhüllenden eines räumlich und zeitlich oszillierenden Wellenpaketes. Wegen dieses universellen Charakters taucht sie in verschiedensten Bereichen, wie beim Wasserwellenproblem oder in der Nichtlinearen Optik, als Amplitudengleichung auf. In numerischen Simulationen erweist sie sich als hervorrangende Approximation der Wirklichkeit, die vielfach weit über den theoretischen Gültigkeitsbereich praktisch anwendbar ist. Das Ziel dieses Projektes soll der Nachweis oder die Falsifizierung der Approximationseigenschaft der NLS-Gleichung für semilineare Systeme mit instabilen quadratischen Resonanzen und für quasilineare Systeme mit nichtresonanten quadratischen Nichtlinearitäten sein. Der Nachweis soll durch ein Zusammenspiel numerischer und analytischer Methoden geschehen.

Graduiertenkolleg GRK 1294/1: Analysis, Simulation und Design nanotechnologischer Prozesse
Das Graduiertenkolleg ist am Karlsruher Institut für Technology angesiedelt. Weitere Informationen 

• Antragsteller:  Prof. Dr. Guido Schneider und PD Dr. Hannes Uecker
• Projektbearbeiter:  von Oktober 2006 bis Februar 2010 Tobias Häcker
• Laufzeit: 10/2006 - 9/2009
• Zusammenfassung: Viskose Flüssigkeitströmungen mit freiem Rand über periodisch gewellte geneigte Böden treten in einer Vielzahl von technologisch wichtigen Bereichen auf, z.B. bei Beschichtungs- oder Kühlungsvorgängen. Sie bilden vielfältige Oberflächenprofile aus und lassen sich experimentell, numerisch und analytisch untersuchen. Abhängig von den physikalischen Parametern des Systems, der Oberflächenspannung, dem Neigungswinkel, der Viskosität, der Filmdicke und der Welligkeit des Bodens, gilt es, die zugrunde liegenden Navier-Stokes-Gleichungen mit freiem Rand zu analysieren. Ziel des Projektes ist es, analytische Vorarbeiten zu ebenen Böden auf den Fall gewellter Böden zu übertragen. Eine wesentliche mathematische Schwierigkeit liegt im freien Rand, weshalb für die Analysis eine Integralrandschichtgleichung benutzt wird, die als Näherungsgleichung für den Fall dünner Filme aus den Navier-Stokes-Gleichungen hergeleitet wird. Weitere Schwierigkeiten liegen in den periodischen Koeffizienten sowie dem stets vorhandenen kontinuierlichen Spektrum der Linearisierungen bis mindestens an die imaginäre Achse.