Welcome to Timo Weidl's HomePage!

Fakultät für Mathematik und Physik
Institut für Analysis, Dynamik und Modellierung
Universität Stuttgart
Pfaffenwaldring 57
D-70569 Stuttgart
Deutschland
tel.: int+49-711-685 65562
fax: int+49-711-685 65594
weidl@mathematik.uni-stuttgart.de
Zimmer: 8.347

Current teaching

Personal stuff

Scientific interests

Slides of Conference and Colloquium Talks

List of Publications



Current Teaching

Personal stuff



Scientific Interests

Summary: In my scientific research I study problems in mathematical analysis and functional analysis, which arise from mathematical physics. I focus on the spectral analysis of differential and integral operators with applications to quantum mechanics.

Atoms and molecules trap electrons at well-defined energy levels only. The distribution of those eigenvalues has significant impact on the physical properties of the system. Their study is therefore one of the main subjects of mathematical physics.

For sufficiently large structures good approximations for eigenvalues can be derived in the so-called semi-classical limit. It describes how quantum mechanical behaviour will transform into the laws of classical physics. But often such asymptotical calculations extend to relevant information for the actual quantum regime as well. Namely, certain spectral characteristics (number or average of eigenvalues) can be estimated in terms of their classical counterparts (volume or average of phase spaces).

The respective results are reflected in the so-called Cwikel-Lieb-Rosenblum and Lieb-Thirring inequalities. Providing an intrinsic connection bewteen classical mechanics and "real" quantum physics, they are of principal importance. They find numerous applications, for example, in the quantum theory of many-body systems or in hydrodynamics. As a main line in my research I have contributed to the theory of these inequalities [4,5,6,10,13,14,15,18,23,24]. One should point out the results of [13,14], where we derive optimal constants or give significant improvements thereof.

In [3,8] we have studied Schrödinger type operators with periodic structures. These simulate the behaviour of electrons in crystals. Given impurities, electrons can form bound states at otherwise "forbidden" energies. We have shown, that for large localized perturbations the number of new energy levels does essentially not depend on the particularities of the structure of the crystal or external electric or magnetic fields.

In the paper [9] I study, whether an arbitrary small perturbation of a physical system will always lead to the trapping of particles (appearance of virtual bound states). The impact of magnetic fields on this effect is the subject of [11,12]. Virtual bound states are also one of the mathematical origins for the trapping effects in slightly deformed wave-guides. In [9,21] we give a justification for the so-called edge resonance states in elastic wave-guides.

Ideals of compact operators form a powerful technical tool to analyse eigenvalue distributions of partial differential operators. In [1,2] I have studied certain generalisations of weak Neuman-Schatten ideals. Applications to Cwikel's theorem can be found in [4,10,18,22].



Slides of Some Conference and Colloquium Talks



List of Publications
  1. T. Weidl: ``Some general operator ideals of the weak type'', (Russian) Algebra i Analiz, 4, 3 (1992) 117-144, (English) AMS St.-Petersburg Mathematical Journal, 4, 3 (1993) 503-525.
  2. T. Weidl: ``Estimates for operators of the type b(x)a(D) in non-powerlike ideals'', (Russian) Algebra i Analiz, 5, 5 (1993) 48-67, (English) AMS St.-Petersburg Mathematical Journal 5, 5 (1994) 907-923.
  3. M. Sh. Birman, T. Weidl: ``The discrete spectrum in a gap of the continuous one for compact supported perturbations'', Operator Theory: Advances and Applications, 70 (1993) 9-12.
  4. T. Weidl: ``Cwikel type estimates in nonpower ideals'', Mathematische Nachrichten, 176 (1995) 315-334.
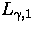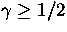  5. T. Weidl: ``On the Lieb-Thirring constants $L_{\gamma,1}$ for $\gamma\geq 1/2$'', Communications in Mathematical Physics, 178, 1 (1996) 135-146.
  6. Y. Netrusov, T. Weidl: ``On Lieb-Thirring inequalities for higher order operators with critical and subcritical powers'', Communications in Mathematical Physics, 182, (1996) 355-370.
  7. I. Roitberg, D. Vassiliev, T. Weidl: ``Edge resonance in an elastic semi-strip'', Quaterly Journal of Mechanics and Applied Mathematics, 51 (1998) 1-13.
  8. T. Weidl: ``Eigenvalue asymptotics for locally perturbed second order differential operators'', Journal of the London Mathematical Society 57 1 (1999) 227-251.
  9. T. Weidl: ``Remarks on virtual bound states for semi-bounded operators'', Communications in Partial Differential Equations 24 1&2 (1999) 25-60.
  10. T. Weidl: ``Another look at Cwikel's inequality'', in Differential Operators and Spectral Theory. M.Sh. Birman's 70th Anniversary Collection. AMS Translations Series 2 189 (1999) 247-254.
  11. A. Laptev, T. Weidl: ``Hardy inequalities for magnetic Dirichlet forms'', Operator Theory: Advances and Applications 108 (1999) 299-305.
  12. T. Weidl: ``A Remark on Hardy type inequalities for critical Schrödinger operators with magnetic fields'', Operator Theory: Advances and Applications 110 (1999) 345-352.
  13. A. Laptev, T. Weidl: ``Sharp Lieb-Thirring Inequalities in High Dimensions'', Acta Mathematica 184 (2000) 87-111.
  14. D. Hundertmark, A. Laptev, T. Weidl: ``New bounds on the Lieb-Thirring constants'', Inventiones mathematicae 140 3 (2000) 693-704.
  15. A. Laptev, T. Weidl: ``Recent results on Lieb-Thirring inequalities'', Proceedings Journees EDP 5-9 juin 2000 (2000) XX-1 - XX-14
  16. P. Exner, T. Weidl: ``Lieb-Thirring Inequalities on Trapped Modes in Quantum Wires'', XIIIth International Congress on Mathematical Physics (London, 2000), 437-443, Int. Press, Boston, MA, 2001.
  17. A. Laptev, O. Safronov, T. Weidl: ``Bound state asymptotics for elliptic operators with strongly degenerated symbols'', Nonlinear problems in mathematical physics and related topics, I, In Honor of Professor O. A. Ladyzhenskaya. 233-246, Int. Math. Ser. (N. Y.), 1, Kluwer/Plenum, New York, 2002.
  18. S. Vugalter, T. Weidl: ``On the Discrete Spectrum of a Pseudo-Relativistic Two-Body Pair Operator'', Ann. Henri Poincaré 4 (2003), no. 2, 301-341.
  19. P. Exner, H. Linde, T. Weidl: ``Lieb-Thirring inequalities for geometrically induced bound states'', Lett. Math. Phys. 70 (2004), no. 1, 83-95.
  20. Spectral analysis of partial differential equations. Abstracts from the workshop held November 28--December 4, 2004. Organized by Alexander V. Sobolev and Timo Weidl. Oberwolfach Reports. Vol. 1, no. 4. Oberwolfach Rep. 1 (2004), no. 4, 2839--2911.
  21. C. Förster, T. Weidl: ``Trapped modes for an elastic strip with perturbation of the material properties'', Quaterly Journal of Mechanics and Applied Mathematics 2006 59(3), 399-418.
  22. T. Weidl: ``Nonstandard Cwikel Type Estimates''. 337--357, Contemp. Math., 445, Amer. Math. Soc., Providence, RI, 2007.
  23. H. Kovarik, S. Vugalter, T. Weidl: ``Spectral estimates for two-dimensional Schrödinger operators with application to quantum layers''. Comm. Math. Phys. 275 (2007), no. 3, 827--838.
  24. R. L. Frank, B. Simon, T. Weidl: ``Eigenvalue Bounds for Perturbations of Schrödinger Operators and Jacobi Matrices With Regular Ground States.'' Comm. Math. Phys. 278 (2008), no. 1, 199--208.
  25. T. Weidl: ``Improved Berezin-Li-Yau inequalities with a remainder term'', in Spectral Theory of Differential Operators, Amer. Math. Soc. Transl. (2) 225 (2008), 253--263.
  26. R. L. Frank, M. Loss, T. Weidl: ``Polya's Conjecture in the Presence of a Constant Magnetic Field''. JEMS 11 (2009) 1365-1383.
  27. H. Kovarik, S. Vugalter, T. Weidl: ``Two-dimensional Berezin-Li-Yau inequalities with a correction term''. Comm. Math. Phys. 287 (2009) no. 3, 959--981.



visitors since November 3rd, 1997.



A Mathematician is a machine for turning coffee into theorems. P. Erdös